Uniqueness check in Ethereum contracts using bloom filters

Last modified on 2024-02-04

In this article, we will explore a duplicate detection algorithm using modified Bloom filters. We will also demonstrate the scalability of the bloom filter method by performing probabilistic analysis.

Naive algorithm for checking duplicates

It is common for an Ethereum contract to require that a supplied set of items has no duplicates. For example, a multi-asset decentralized exchange might run price quoting calculations using algorithms that require no items are repeated. In general, such a decentralized exchange would compare each item with all other items to ensure there are no duplicates. Such a function might look like below.

function swap(ItemERC20[] calldata payments, ItemERC721 calldata purchase) external {

    // Disallow duplicate tokens.
    for (uint256 i = 0; i < payments.length; ++i) {
        for (uint256 j = i + 1; j < payments.length; ++j) {
            if (payments[i].token == payments[j].token) {
                error DuplicateItems();
            }
        }
    }

    /* Assume rest of the function here */

}

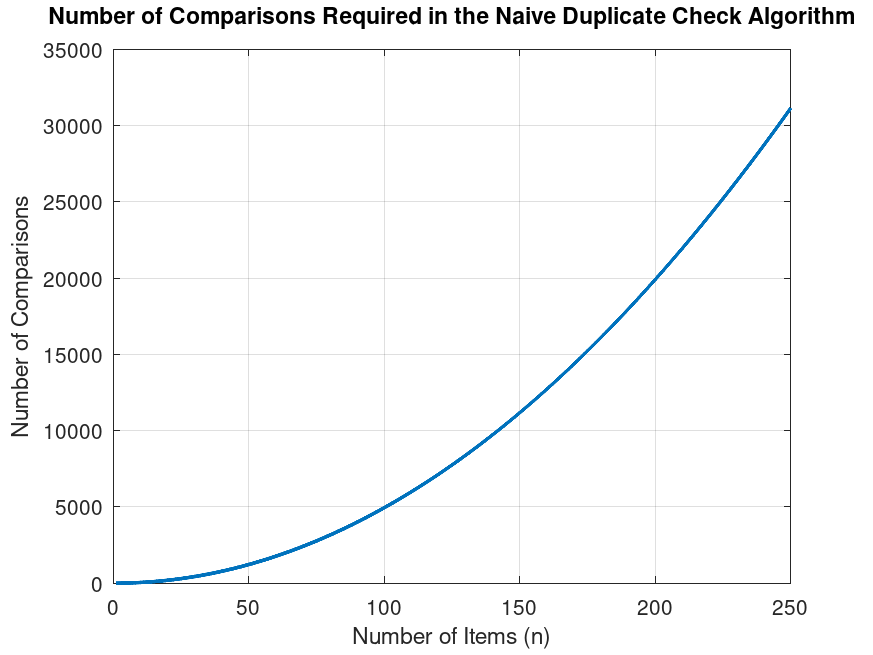
This approach, which we will call the naive algorithm, is simple and effective, but it has a non-linear increase in complexity as the item count increases. The time complexity of this algorithm can be given by the formula $$ O\left(\sum_{i=1}^{n}{(i-1)}\right) $$ where n is the number of items. This method is impractical for large arrays. For example, for 10 items, there will be 45 loop iterations, which may be acceptable. However, for 100 items, there will be 4950 loop iterations, which is nearly impractical on Ethereum due to gas limit. Below plot shows the high number of iterations required as the item count increases.

In other programming languages, lookup tables could be used to have an O(n) time complexity. However, in Ethereum, using lookup tables requires using storage, which has a high cost of access. In the future, with the addition of transient storage, using lookup tables might become practical. But transient storage is not that cheap either, and repurposing the transient storage as a lookup table might introduce some security risks. We believe there exists a better solution right now: Bloom filters.

Basic Bloom filter as used in Solidity

A Bloom filter is a probabilistic data structure that is used to test whether an element is a member of a set, allowing for false positive matches but not false negatives. A bloom filter method is already being used by Scribe protocol to detect duplicate addresses given in an array. Below is a refactored and simplified version of Scribe protocol’s bloom filter implementation.

function getSignerId(address signer) internal view returns (uint8) {
    // First byte of an address is its id. There are 256 possible ids ([0x00:0xff]).
    return uint8(uint256(uint160(signer)) >> 152);
}

function checkDuplicates(address[] calldata signers) internal view {
    uint256 bloom = 1 << getSignerId(signers[0]);

    for (uint256 i = 1; i < signers.length; ++i) {
        uint8 id = getSignerId(signers[i]);

        // Revert the exectution if id is already set (means duplicate).
        if (bloom & (1 << id) != 0) error DuplicateSigner();

        // Update bloom filter.
        bloom |= 1 << id;
    }
}

Scribe defines an id of an address as the first byte of the address. Given a byte can be a value between 0 to 255, there are 256 possible ids. It uses a bitmap variable bloom and sets the bit at the location of each id. For example, if the id of an address is 5, it sets the 5th bit of the bitmap variable. If a bit is attempted to be set a second time, that means it is a potential duplicate, and execution reverts. The drawback of this method is that if two different addresses have the same first byte, it would revert with a false positive.

Scribe is not concerned with false positives, because the addresses used in their protocol are generated by them. This allows them to mine addresses with unique initial bytes so that their bloom filter will not produce false positives. But this does not solve the general use case. For example, in the initial exchange example where a user might want to swap using an arbitrary combination of addresses, the transaction would occasionally revert due to false positives.

Scribe’s method falls apart if we decide to use it for arbitrary addresses. Even with only two items, there is a non-negligible possibility of a false positive. This would make this method impractical for most other purposes. Inability to execute a function with certain address pairs would render this method unusable.

To calculate the probability of having no collisions given n items, we assume that byte distribution of addresses is uniform. This might not be the case in practice, due to practices such as vanity address mining. However, the assumption of uniform distribution is reasonable for the analysis. Given the assumption, we can calculate the probability of having no collisions given n items with the formula below.

$$ P_{\text{unique}} = \prod_{i=0}^{n-1} \left(\frac{256-i}{256}\right) $$

The formula is derived by the permutations of n bytes with all unique values being divided by all possible outcomes. Displaying this formula in a graph shows the impracticality of using this method.

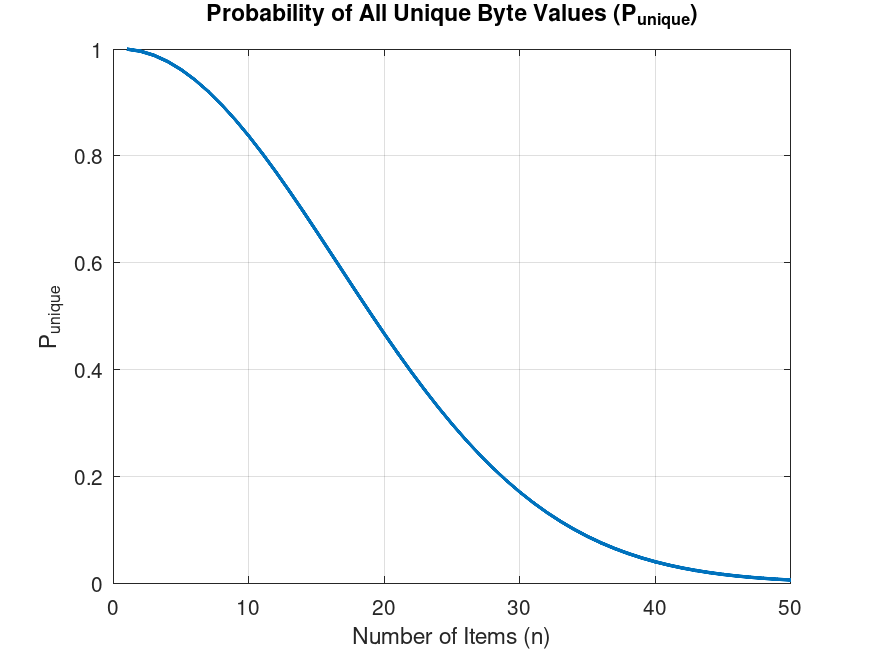
Even at 10 items, there is approximately one-in-five chance of a false positive. At 50 items, there will almost always be a collision. A more advanced approach needs to be developed.

Developing a general bloom filter method using probabilistic analysis

To develop a functional bloom filter method, we will go through step by step and analyze each method’s probability of having a successful solution.

Single nonrandom byte bloom filter

The next addition to developing an efficient bloom filter method would be to allow function callers to specify which byte position they want to use for the bloom filter. For example, along with the addresses, the user would pass a byte position, and that position would be checked for each address. This way, for a 20 bytes value, such as an address, we can use the initial formula 20 times, increasing the probability of finding a byte position with all unique bytes. To derive the formula, we first find the probability of having a collision.

P_collision = 1 − P_unique

Then, we find the probability of all byte positions having a collision, then negate that to find the probability that at least one byte position existing with all unique bytes. Hence the formula becomes

P_success = 1 − (1−P_unique)^p

where p is the possible byte positions (e.g.: 20 for an address list, 32 for a hashed list).

In the below graph, we see the effects of this modification when p=20.

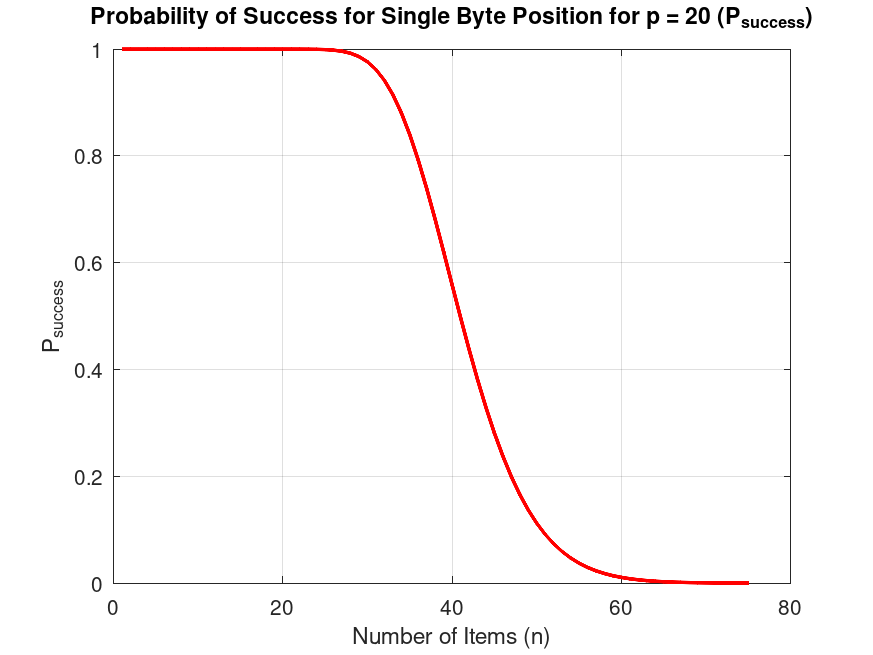
This has significantly improved the probability, especially for low number of items. Approximately up to 20 items, the probability of a collision is negligible. However, as the item count increases we observe the probability rapidly declines. This method is practical for 10 items (P=~1.0000000000), but at 35 items it is completely unusable (P=~0.8397497831).

Interestingly, having a higher selection of bytes than 20 bytes does not have a notable effect. Below is the graph for p=20, p=32, and p=1000.

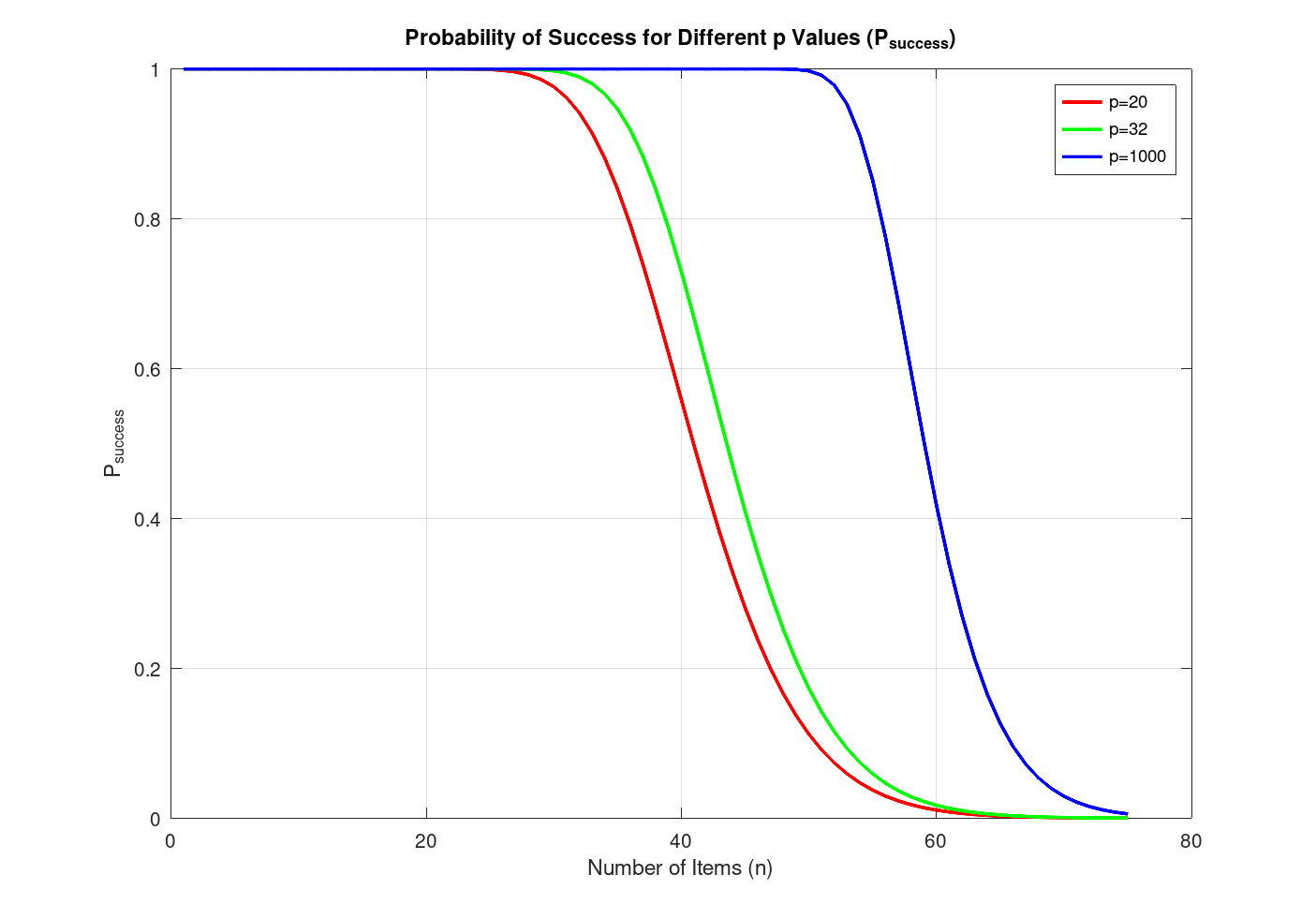
In real Solidity usage it is unlikely to have p>32, let alone p=1000. We added p=1000 to demonstrate its ineffectiveness in improving the probability. It works reliably up until about 40 items, but after that the probability declines rapidly. This is not a satisfying improvement.

Multiple bytes bloom filter

There exists one solution that reliably enables usage of bloom filters for detecting duplicates. That is simply using multiple filters, or in other words, multiple byte positions. In this model, a contract could allow users to pass multiple bloom filters. If there exists no solution for all the byte positions checked for a given item set, the user can supply a second byte position. In that case, the contract would require that all supplied byte positions for any two items must clash for them to be proven duplicate. In simpler words, a user can prove that two items are not duplicate if one of their bytes does not match.

To derive the probability formula for this, we replace instances of 256 in the original formula with 256^m, where m is the number of bytes to check, because 256^m gives the possible number of values for m bytes. We also replace the exponentiation by p with binomial(m, p), because that gives the combination of m bytes we can select from a set of p bytes. The resulting formula is below.

$$ P_{\text{multi}} = 1 - \left(1 - \prod_{i=0}^{n-1} \left(\frac{256^m-i}{256^m}\right)\right)^{\binom{p}{m}} $$

The below graph visualizes using 1, 2, and 3 byte positions when p=20. Note that the probability when m=3 starts its rapid decline roughly around 16000 items, which is beyond the bounds of the graph.

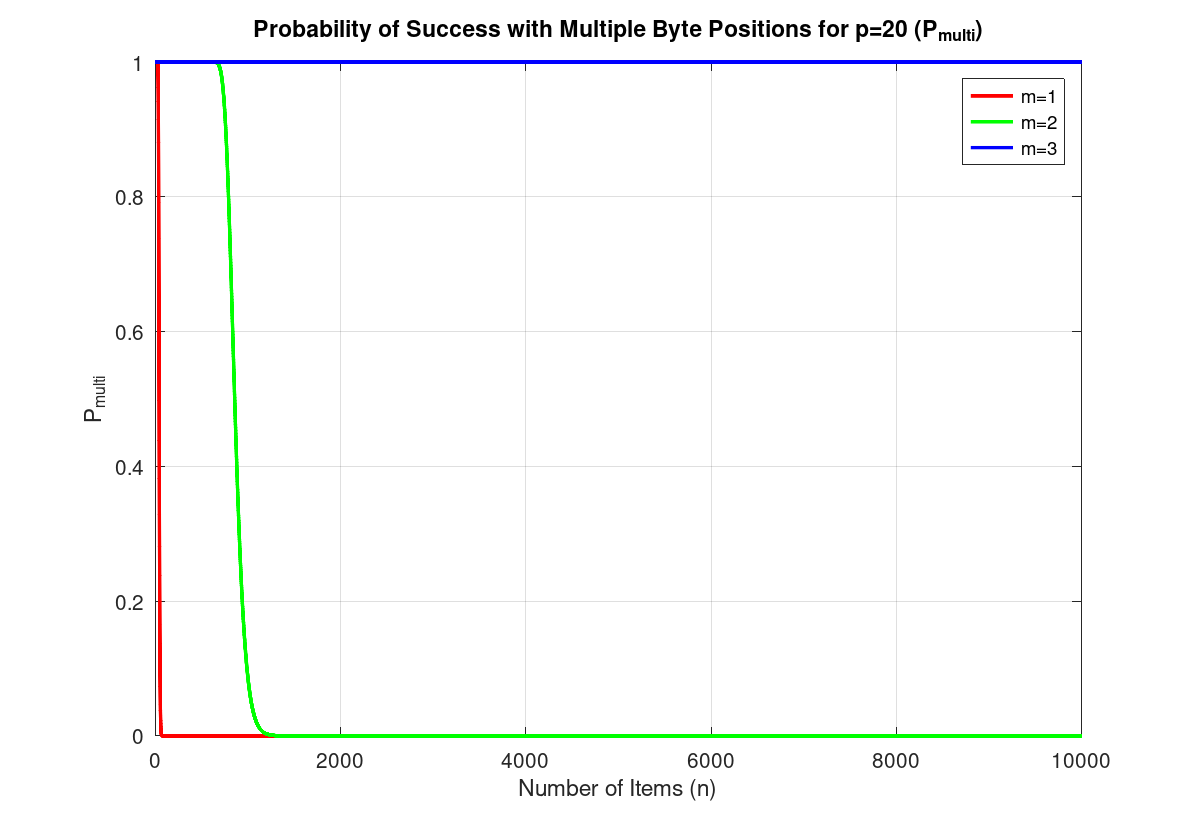
The graph clearly shows the effectiveness of using multiple bloom filters. It is practically impossible for there to be no solution when 3 bloom filters are used, assuming no more than 10000 items are passed. Due to Ethereum block gas limit, loops with 10000 iterations or more would be impossible anyways. Regardless of the practicality, there is no harm in allowing users to pass more than 3 bloom filters. This way, it is guaranteed that a valid proof (i.e.: set of bloom filters) can always be submitted for a given set of unique values.

This method interestingly makes the time complexity probabilistic. Although it is close to O(n) for practical purposes.

Solidity code example

With these information, we can rewrite the initial naive algorithm using the bloom filter method. Below is to demonstrate the idea, and it can be further optimized.

function getBitmap(uint256 bitmap, uint8 index) internal pure returns (bool) {
    return (bitmap >> index) & 1 == 1;
}

function setBitmap(uint256 bitmap, uint8 index) internal pure returns (uint256) {
    return bitmap | (1 << index);
}

function getIndex(address addy, uint8 filter) internal pure returns (uint8) {
    return uint8(uint160(addy) >> filter)) & 0xff;
}

function swap(
    ItemERC20[] calldata payments,
    ItemERC721 calldata purchase,
    uint8[] calldata filters
) external {

    // Disallow duplicate tokens.
    uint256[] memory bitmaps = new uint256[](filters.length);
    for (uint256 i = 0; i < payments.length; ++i) {
        uint256 collisions = 0;
        for (uint256 j = 0; j < bitmaps.length; ++j) {
            uint8 index = getIndex(payments[i].token, filters[j]);
            if (getBitmap(bitmaps[j], index)) ++collisions;
            else setBitmap(bitmaps[j], index);
        }
        if (collisions >= bitmaps.length) error DuplicateItems();
    }

    /* Assume rest of the function here */

}

A more optimized version of this code could use the naive algorithm when it is cheaper to do so, which would likely be the case below a certain item count like 4 or 5. However, that is beyond the scope of this article.

Conclusion

We have demonstrated how to use bloom filters in Solidity to detect duplicates in a list. We have also performed probabilistic analysis on the reliability of using the bloom filter method. The analysis shows that multiple bloom filters can be combined to achieve an efficient and reliable duplicate detection algorithm. More analyses needed on gas comparison of the naive method against the multi bytes bloom filter method. If the gas analysis proves the efficiency of the method, a duplicate detection library in Solidity could be written for all developers to benefit from.